Stress Strain Curve

Load Deformation Curve

Before diving into the stress-strain curve, let's first understand the load-deformation curve. Imagine a prismatic cylindrical bar subjected to a tensile load. If we plot the load applied against the resulting elongation of the bar, we obtain what is known as the load-deformation curve. This curve provides insight into the behavior of the bar under load. However, it does not account for variations in geometry, meaning it cannot predict the deformation for bars of the same material but with different sizes.

For example, consider two bars made of the same material and of equal length, but one has a cross-sectional area of \(A\) and the other has \(2A\). To produce the same elongation \(\delta\), the first bar would require a force \(P\), while the second would require \(2P\).

Similarly, if we take two bars with identical cross-sectional areas and material, but with lengths \(L\) and \(2L\), and apply the same load \(P\), the shorter bar will elongate by \(\delta\), while the longer one will elongate by \(2\delta\).

If you’ve been following the previous tutorials closely, you might have noticed that in the first example, the applied stress was the same for both bars, and in the second example, the resulting strain was identical.

Stress-Strain Curve

The stress-strain curve is a plot that shows the relationship between the stress and strain of a prismatic bar. The stress can be applied as tension, compression, or shear. However, in most cases, the stress-strain curve refers specifically to tensile stress and strain. From this curve, we can derive important physical properties of a material such as elastic limit, yield strength, Young’s modulus, ultimate tensile strength, toughness, resilience, ductility, and more.

Regions of the Stress-Strain Curve

To understand the different regions, we will refer to the stress-strain curve of mild steel.

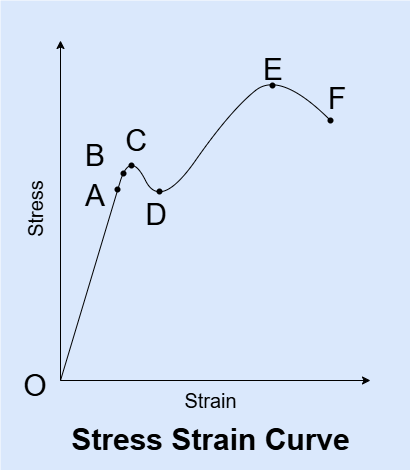
Let’s begin by identifying key points on the stress-strain curve:

1. O - This is the origin point of the curve, where both stress and strain are zero.
2. A - Point A marks the proportional limit. Up to this point, stress and strain increase linearly, and Hooke’s Law is valid.
3. B - This point represents the elastic limit of the material. Up to point B, the material will return to its original shape when the load is removed.
4. C - This is the upper yield point, where plastic deformation begins.
5. D - The lower yield point. During yielding, molecular bonds break and new ones form. In this region, the material continues to deform even if the stress slightly decreases.
6. E - This point represents the ultimate tensile strength — the maximum stress the material can withstand before necking begins.
7. F - This is the fracture or failure point, where the material breaks into two pieces.

Now let’s explore the various regions of the stress-strain curve:

1. Proportional Limit Region (O-A) - In this region, stress and strain maintain a linear relationship, and Hooke’s Law applies.
2. Elastic Limit Region (O-B) - Within this region, the material behaves elastically. Removing the load will allow the material to return to its original shape.
3. Elasto-Plastic Region (B-C) - The material exhibits both elastic and plastic behavior. Upon load removal, it will partially recover but also show permanent deformation.
4. Yielding Region (C-D) - From point C (upper yield point) to D (lower yield point), the material undergoes plastic deformation. In this stage, internal grain structures shift and dislocations occur.
5. Strain Hardening (D-E) - This region is known as strain hardening. The interlocking of dislocations leads to increased material strength.
6. Necking (E-F) - In this region, the cross-sectional area reduces significantly, forming a "neck" that eventually leads to failure.
7. Plastic Region (D-F) - Throughout this region, the material exhibits plastic behavior. Removing the load will not allow the material to return to its original shape.